こんにちは。鎌田です。

今回は、高校入試でよく出題される「規則性」の問題を取り上げ、早い段階からの訓練の大切さについて話していきたいと思います。

「規則性」に関する問題は、問題によって規則のパターンがさまざまで、すべてのパターンをマスターするのはなかなか難しいでしょう。しかし、入試で得点率が低いことが多いこの部分の出来が合否を左右することがあるのも事実です。

そこで、『光の泉』では、多様な「規則性」に対応する力をつけていくために、同じ問題をいろいろな方法で解き、さまざまな角度から柔軟に問題を見る力を養っています。比較的やさしい問題を例に見ていきましょう。

(例)　図のように、マッチ棒を並べていきます。正方形の数がn個であるとき、マッチ棒の本数を、nを使った式で表しなさい。

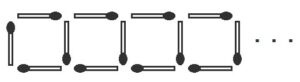
〈解き方１〉「表を書く」

マッチ棒が3本ずつ増えていることがわかります。1個からｎ個になるまでに(ｎ-1)回増えるので、4+3(ｎ-1)という式がつくれます。これがもっとも一般的な解き方です。

〈解き方２〉「図形から考える」

新しく加えていく部分の形に注目すると、下の図のように分けることができます。

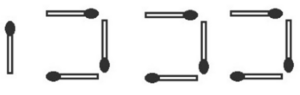
左端の1本と、「コ」の字形の３本部分がｎ個と考えられるので、3ｎ+1という式ができます。

このように、『光の泉』の小学生には、さまざまなアプローチの仕方を指導しています。早い段階から訓練を繰り返すことで、将来、入試で出題されるもっと複雑な問題に対応する力がどんどんついていきます！ 岐阜高校を目指したい子は、『光の泉』の難しい算数で鍛えてみませんか！

9月10日より、土曜講座「土スク」がスタートします。

「岐阜高校に上位で合格したい」、「難関私立高校に挑戦したい」と考えている中１・２の方にお勧めの講座です。

くわしくはコチラ！！

↓↓↓

土曜講座「土スク」