2024.11.20

2024.11.16

2024.11.13

2024.11.10

2024.11.07

2022.07.05|算数　難問解説

こんにちは。講師の近藤です！

光の泉では、小学生の時から、柔軟な発想が求められる問題にチャレンジしていきます。

今回は、小学6年生の生徒たちがチャレンジした問題を見ていきたいと思います。

皆さんも挑戦してみてください！

問.半径７㎝の円に、ぴったりと入る正十二角形の面積は何㎠ですか。

～解説～

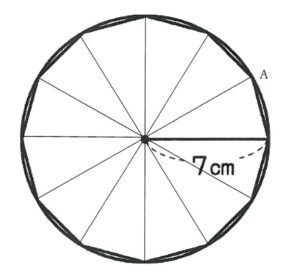
①中心をO、1つの頂点をAとして直線を引く。

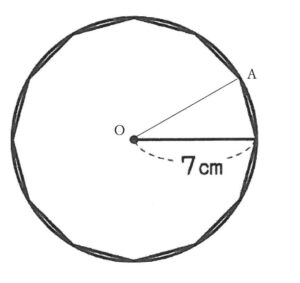
②各頂点に同じように直線を引く。

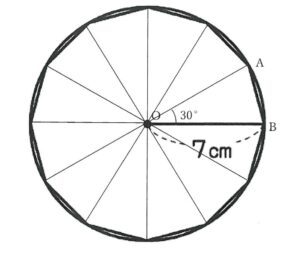
各頂点に同じように直線を引くと、合同な二等辺三角形が12個できる。（360°を12等分したので1つの角の大きさは30°）

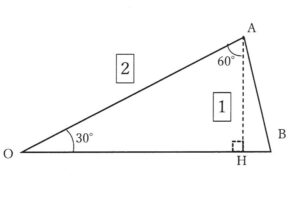
→三角形OABの面積を求めて12倍すれば正十二角形の面積が求められる！

③三角形OABの面積を求める。

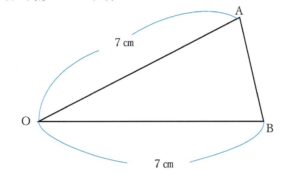
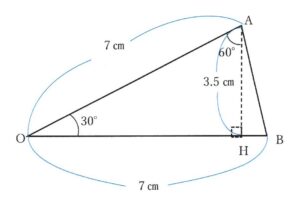
★三角形OABに注目

半径は７㎝なので、OA=OB=７㎝。

あとは、高さが分かれば三角形OABの面積が求められる。

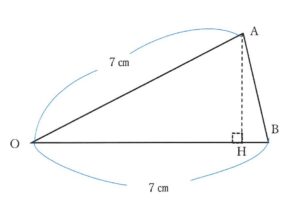
頂点Aから辺OBに向かって垂線を引き、ＯＢとの交点をＨとする。ＡＨの長さ＝三角形OABの高さなのでＡＨを求める。

④AHを求める。

★三角形OAHに注目

三角形OAHの角度は30° 90° 60°になっている。

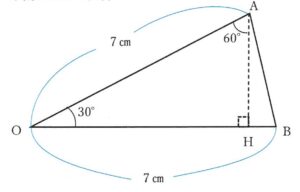
角度が30° 90° 60°の三角形には、最も長い辺：最も短い辺＝２：１という特徴がある。三角形OAHではOA:AH＝２：１

OAは７㎝なので、OA:AH＝２：１よりAHは3.5㎝とわかる。

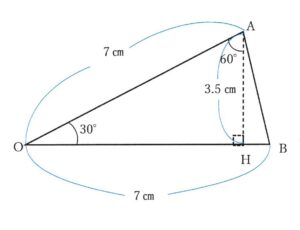
⑤正十二角形の面積を求める。

三角形OABの高さ＝3.5㎝だと分かったので、三角形OABの面積は７×3.5÷２で求められる。

三角形OABと合同な二等辺三角形が12個あるので、7×3.5÷2×12を計算して、147㎠が答えとなる。

光の泉では小学生のうちから難易度の高い算数の問題をこなし、中学生にあがる段階で他の生徒と大きく差をつけます。

算数・数学の力を伸ばしたいという方には、光の泉がおすすめです！

光の泉では「後期入塾生」募集中！！詳しい内容はコチラから！

↓↓↓