前回のブログで，以下の問題を出題しました。

問題

３０！＝１×２×…×２９×３０は，３で何回割り切ることができますか。

では，解説します。

ヒントとして，１０！＝１×２×３×４×５×６×７×８×９×１０が，

３で４回割り切れることを書きましたが，

この理由を考えると，問題の答えが分かってきます。

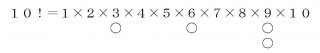
上の○は３で割り切れる理由となる部分を表していて，全部で４つあります。

なぜ，４つなのかというと，１から１０までの中に，

３の倍数が３個，９（＝３×３）の倍数が１個あるからです。

（計算　１０÷３＝３…１，１０÷９＝１…１）

したがって，問題の答えは，１から３０までの中にある３の倍数，

９の倍数，２７（＝３×３×３）の倍数の個数を合計すれば，求めることができます。

３０÷３＝１０，３０÷９＝３…３，３０÷２７＝１…３なので，

１０＋３＋１＝１４，つまり，３で１４回割り切れることが分かります。

なお，多少，問題の表現は異なっていますが，２０１０年の東北学院大の入試で，

「１００！は，３で何回割り切ることができますか。」

という問題が出題されています。

さあ，それでは，本題に入りましょう。

問題

９９！の末尾には０が何個ならぶか。（２００９年，明海大）

答えが分かった人は，今回の説明を参考にして，

答えとその理由を紙に書いて，高橋まで提出して下さい。

正解者には，先着３名まで（各学年１名まで）に，

ＫＡＺＡＳＵポイント５０ポイントを差し上げます。

がんばって考えてください。

追伸

お盆休みに，知多半島に出かけました。

そのときに，撮ってきた海と空の写真です。

2011-08-22　　　高橋